Redes ópticas de alto desempenho: Entenda a modelagem de constelação probabilística
A PCS – modelagem de constelação probabilística permite que um determinado transponder forneça uma combinação de taxa de dados de comprimento de onda e alcance óptico próximo ao limite da capacidade teórica de transmissão do cabo.
Geoff Bennett, diretor de soluções e tecnologia, da Infinera
A PCS – Modelagem de constelação probabilística é a próxima grande novidade na transmissão coerente de alto desempenho em redes ópticas. A promessa da PCS é que ela permitirá que um determinado transponder forneça uma combinação de taxa de dados de comprimento de onda e alcance óptico próximo ao limite da capacidade teórica de transmissão do cabo (também conhecido como limite de Shannon).
Deixe-me lembrá-los brevemente de como funciona a modelagem de constelação probabilística e, em seguida, irei explicar um dos recursos mais importantes para uma implementação da PCS eficaz: “palavras-código longas”.
À medida que você aumenta a ordem de modulação (por exemplo, de QPSK até 64QAM), o alcance óptico cai exponencialmente, enquanto a eficiência espectral aumenta de forma muito moderada.
Mas operar com a modulação mais alta que você pode usar para um determinado alcance é uma maneira vital de reduzir o custo por bit na rede e maximizar a capacidade da fibra, portanto, uma boa parte do projeto da rede é maximizar a ordem de modulação. A PCS soluciona esse problema.
Se usarmos a modulação discreta (o resultado é mostrado na figura abaixo), existe um efeito “dente de serra” quando o transponder muda de uma modulação para outra. A figura também indica uma linha pontilhada representando o limite de Shannon – se você operar o link próximo a uma das quedas no “dente de serra”, como efeito você estará mais longe do limite de Shannon.
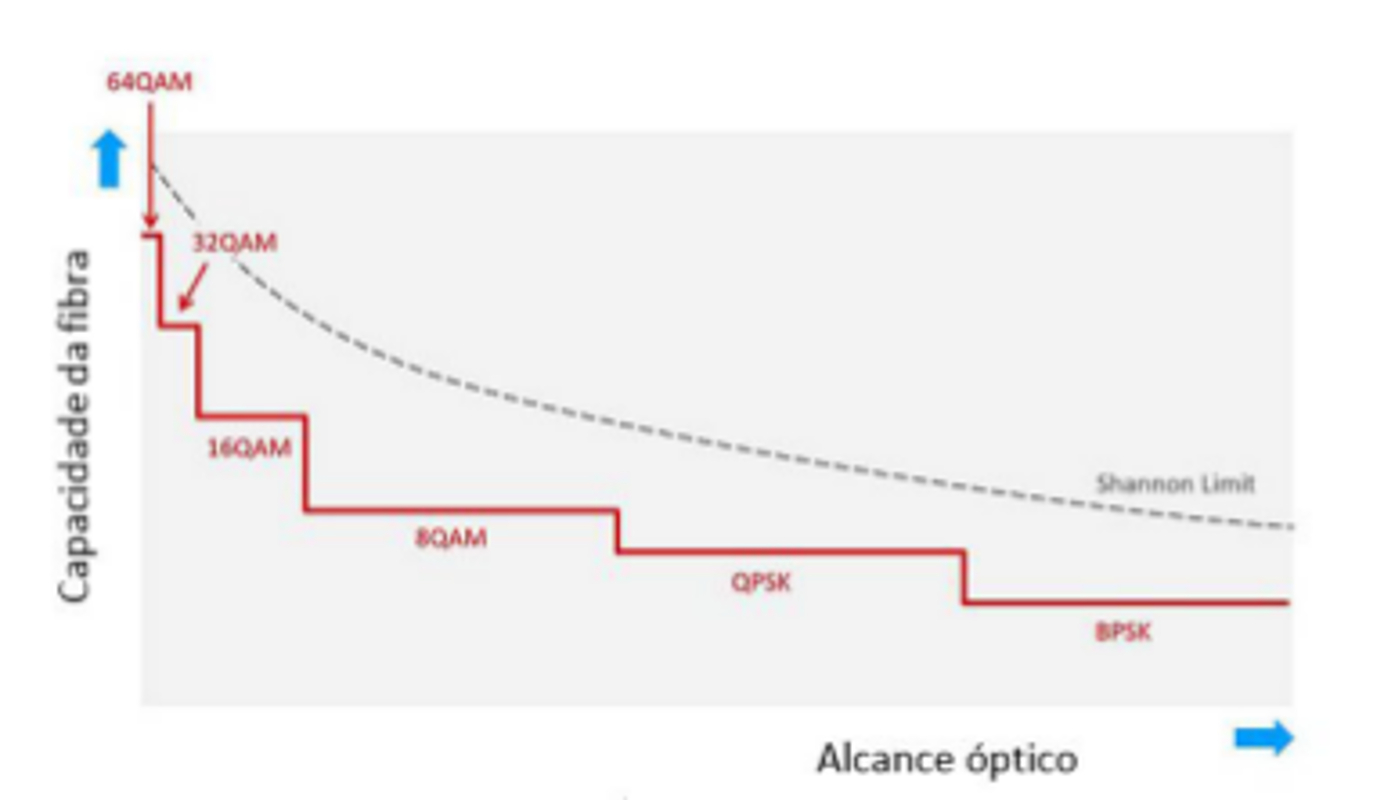
A figura abaixo aponta que a PCS começa com uma constelação completa de 64QAM. Estou mostrando apenas uma polarização para simplificar. Em distâncias curtas podemos usar a constelação completa e um sinal PM-64QAM carregará 12 bits de dados.
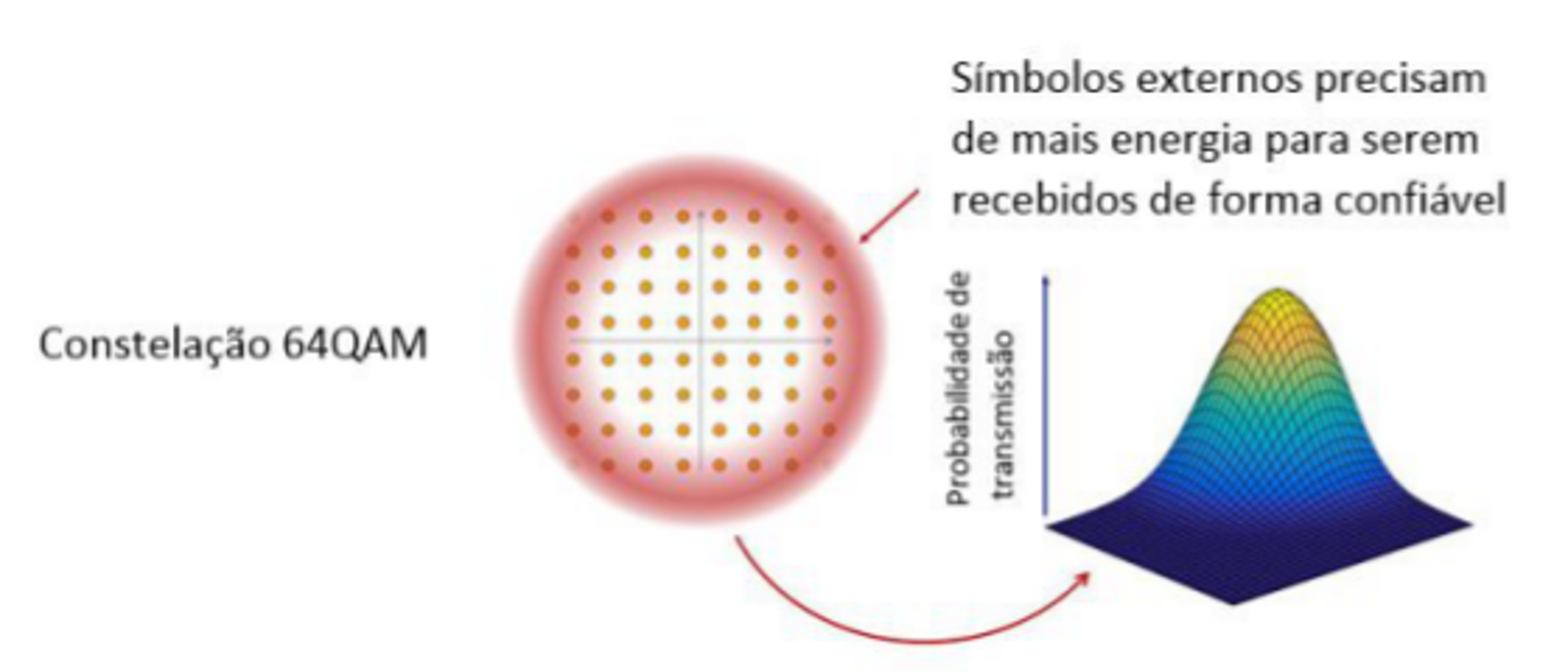
No entanto, as localizações dos símbolos externos destas constelações se tornam mais desafiadoras para um receptor detectar de forma confiável à medida que o alcance aumenta. Portanto, o que a PCS faz é reduzir a probabilidade desses símbolos externos serem usados para codificar dados, além de aumentar a probabilidade dos símbolos internos serem utilizados. À direita da figura 2 você pode ver um mapa de probabilidade 3D, onde a forma ideal segue uma distribuição gaussiana.
Um ponto fundamental é que essas probabilidades podem ser alteradas mais facilmente do que alternar entre modulações rígidas e, na figura 1, o resultado será suavizar a forma do “dente de serra” da curva. Observe que ainda haverá um “dente de serra”, mas será muito mais fino porque a sua granularidade agora é determinada pela necessidade de mapear taxas de dados discretas do cliente no comprimento de onda.
O efeito colateral desta manipulação de probabilidade é que haverá menos bits disponíveis por símbolo, onde o transponder pode fazer o mapeamento do fluxo de dados.
O que é uma “palavra-código” de PCS, afinal?
As implementações de PCS incluem um algoritmo de mapeamento que tentará garantir que o maior número de bits por símbolo esteja disponível para um determinado nível de desempenho óptico.
Este mapeamento é mais eficiente quanto mais o algoritmo puder olhar para o próximo fluxo de dados. A analogia que eu usaria seria um programa de xadrez. Segundo a Wikipédia, a maioria dos desenvolvedores de software de xadrez concorda que é necessário olhar pelo menos cinco jogadas à frente para que se possa jogar bem. Mas, em média, existem mais de 30 movimentos legais de xadrez a partir de qualquer posição, portanto, um computador que esteja olhando cinco jogadas à frente teria que examinar um quatrilhão de jogadas possíveis! O software de xadrez usa técnicas inteligentes para reduzir drasticamente esse número, mas o princípio fundamental é verdadeiro.
Alguns fornecedores já anunciaram implementações de PCS com “palavras-código” bastante curtas, mas o que isso significa na prática? Como o algoritmo da PCS não tem a chance de examinar profundamente o fluxo de dados, há uma probabilidade maior de que ele seja forçado a mapear um conjunto específico de bits em um dos símbolos externos da constelação, o que reduziria o alcance desses bits, assim como qualquer outro bits que sofra um destino semelhante.
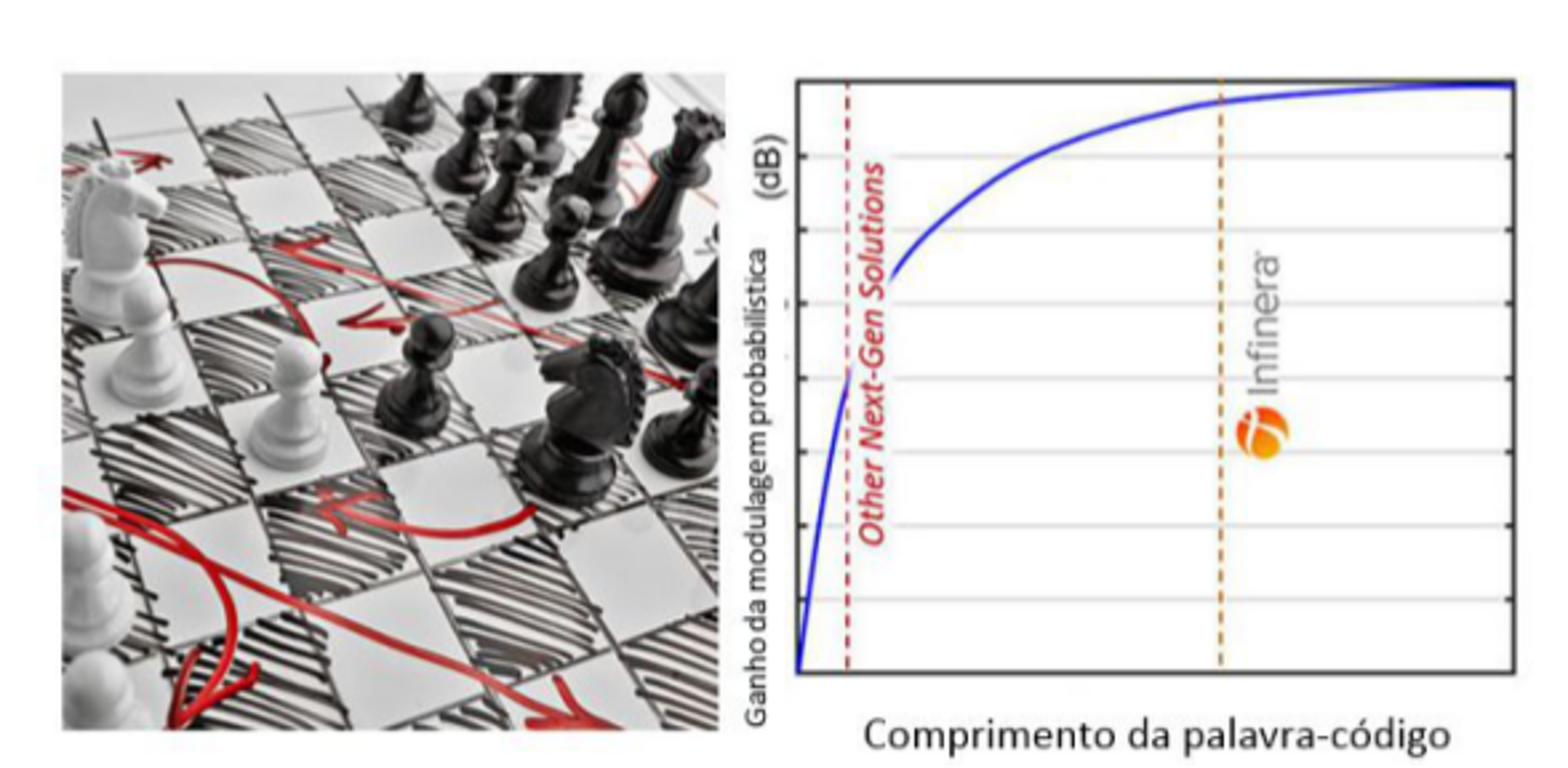
Em nossa análise inicial da PCS, identificamos rapidamente a importância do comprimento da “palavra-código”. A figura 3 mostra o benefício da PCS para a tolerância da relação sinal-ruído expressa em função do comprimento da “palavra-código”.
Armados com esse resultado, seguimos em direção a uma implementação que proporciona essencialmente todos os benefícios potenciais. Para soluções concorrentes, vemos que elas impuseram restrições ao comprimento da “palavra-código”, o que significa que quase metade do benefício é perdido.
Inicialmente, estávamos preocupados que a escolha de uma “palavra-código” mais longa tivesse um grande impacto na complexidade da implementação e na dissipação de energia. Felizmente, conseguimos otimizar esse algoritmo complicado, de tal forma que a dissipação geral de energia dentro dos principais blocos da PCS em nosso mecanismo de capacidade infinita de sexta geração (ICE6) é uma fração minúscula da energia total. E, caso você esteja se perguntando, aumentar o comprimento da “palavra-código” não tem um efeito perceptível na latência, o que é realmente uma vantagem para todos.










